Бесконечная последовательность квадратов.

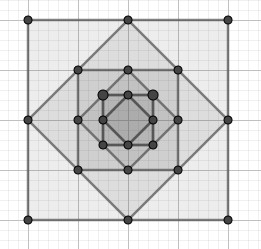
На рисунке изображена бесконечная последовательность квадратов, вписанных друг в друга таким образом, что вершины каждого последующего квадрата совпадают с серединами сторон предыдущего квадрата. Сторона самого большого квадрата имеет единичную длину. Чему равна площадь всей бесконечной последовательности квадратов?

Ответ

Решение задачи

Площадь самого большого квадрата равна 1²=1. Сторона каждого нового квадрата равна квадратному корню из суммы квадратов половинных сторон большего квадрата. Для второго квадрата сторона равна √(1/2²+1/2²)=√1/2 , а площадь 1/2. Таким образом, площадь всей бесконечной последовательности квадратов равна 1 плюс сумма ряда 1/2 + 1/4 + ... Обозначим ряд через х и, поскольку каждый член этого ряда в 2 раз меньше предыдущего, умножим обе части получившегося равенства на 2:
x = 1/2 + 1/4 + 1/8 + ...
2x = 1 + 1/2 + 1/4 + ...
2x = 1 + x, x = 1.
Таким образом, сумма этого ряда равна 1. Иными словами, полная площадь, занимаемая членами бесконечной последовательности квадратов, равна 1 + 1 = 2.

О задаче

Категория: Геометрические задачи, Ряды,
Степень сложности: сложная.
Ключевые слова: 1, квадрат,
Источник: Математические новеллы,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

В 10-этажном доме на первом этаже живет 1 человек, на втором - 2, на третьем - 3 и т.д. на десятом - 10. На каком этаже лифт останавливается чаще всего?

a) На десятом этаже.
b) На первом этаже.
c) Примерно одинаково на всех этажах.
d) На пятом этаже.