Двенадцать монет, одна фальшивая, три взвешивания.

Есть 12 монет, одна из которых фальшивая. При этом неизвестно, в какую сторону она отличается от настоящих, т.е. она может быть как легче, так и тяжелее. В вашем распоряжении чашечные весы без гирь. Нужно за три взвешивания найти фальшивую монету, а также выяснить, тяжелее она или легче.

Ответ

Монеты разделяем на три группы по четыре монеты. Далее, используем часть монет в качестве эталонных гирек.

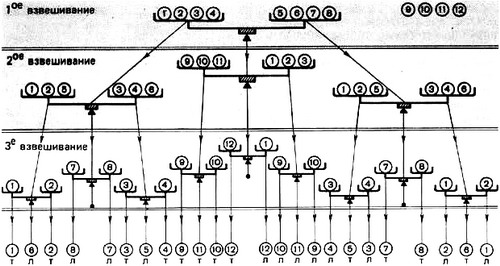
Решение задачи

Для удобства пронумеруем монеты от 1 до 12. Первым взвешиванием сравним две группы по четыре монеты: 1,2,3,4 и 5,6,7,8.
Случай I: первое взвешивание показало равенство. Если весы покажут равенство, то фальшивая монета находится среди оставшихся четырех монет. Тогда вторым взвешиванием мы сравним три монеты 9, 10, 11 с заведомо настоящими 1, 2, 3. Если и в этот раз весы покажут равенство, то фальшивка - монета номер 12, и третьим взвешиванием мы сравним ее с настоящей и узнаем, легче она или тяжелее. Если же три монеты 9, 10, 11 оказались легче (тяжелее), то третьим взвешиванием сравним друг с другом монеты 9 и 10. Если они равны, то монета 11 - фальшивая, и она легче (тяжелее) настоящей. Иначе заключаем, что из монет 9 и 10 фальшивая та, которая легче (тяжелее) другой.
Случай II: первое взвешивание показало неравенство. Теперь предположим, что первое взвешивание показало, что монеты 1, 2, 3, 4 тяжелее, чем 5, 6, 7, 8. Случай, когда первые монеты оказались легче, симметричен. Во втором взвешивании на одну чашу поместим монеты 1, 2, 5, а на другую - монеты 3, 4, 9 (монета 9 - заведомо настоящая). Если второе взвешивание показало равенство, то у нас остаются три монеты 6, 7, 8, одна и которых легче остальных. Третьим взвешиванием сравниваем монеты 6 и 7. Если они равны, то монета 8 легче остальных. Иначе фальшивой является та, которая легче другой. Теперь предположим, что во втором взвешивании монеты 1, 2, 5 оказались тяжелее, чем 3, 4, 9. Это означает, что фальшивка находится среди монет 1 и 2, причем она тяжелее остальных. Сравнив в третьем взвешивании эти две монеты друг с другом, мы определим фальшивую. Предположим, что во втором взвешивании монеты 1, 2, 5 оказались легче, чем 3, 4, 9. Это означает, что либо монета 5 легче остальных, либо одна из монет 3 и 4 тяжелее остальных. Третьим взвешиванием мы сравним друг с другом монеты 3 и 4 и найдем ответ.

О задаче

Категория: Задачи на взвешивание,
Степень сложности: сложная.
Ключевые слова: 3, 12, весы, взвешивание, монета, фальшивка,
Источник: Задачи, ребусы, головоломки стран мира, Математическая смекалка, Математические игры и развлечения, Избранные задачи и теоремы элементарной математики,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Куб, поверхность которого окрашена в черный цвет, разделили шестью разрезами на одинаковые кубики меньшего размера. Сколько кубиков будут иметь по 2 окрашенные грани?

a) 12
b) 27
c) 0
d) 8