Задачи о прыгающем мяче.

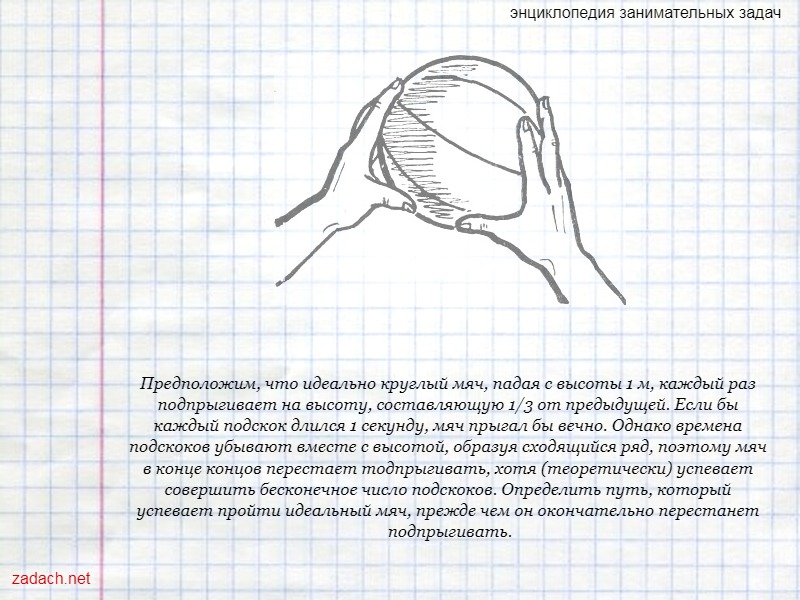
Предположим, что идеально круглый мяч, падая с высоты 1 м, каждый раз подпрыгивает на высоту, составляющую 1/3 от предыдущей. Если бы каждый подскок длился 1 секунду, мяч прыгал бы вечно. Однако времена подскоков убывают вместе с высотой, образуя сходящийся ряд, поэтому мяч в конце концов перестает тодпрыгивать, хотя (теоретически) успевает совершить бесконечное число подскоков. Определить путь, который успевает пройти идеальный мяч, прежде чем он окончательно перестанет подпрыгивать.

Ответ

2 м.

Решение задачи

Когда подпрыгивающий мяч остановится, пройденный им путь будет равен 1 м (высота, с которой он был брошен) плюс сумма ряда (1/3+1/3) + (1/9+1/9) + ... = 2/3 + 2/9 + 2/27 + ... Обозначим ряд через х и, поскольку каждый член этого ряда в 3 раз меньше предыдущего, умножим обе части получившегося равенства на 3:
x = 2/3 + 2/9 + 2/27 + ...
3x = 2 + 2/3 + 2/9 + 2/27 + ...
3x = 2 + x, x = 1.
Таким образом, сумма этого ряда равна 1. Итак, когда, совершив бесконечное число подскоков, мяч остановится, пройденный им путь будет равен 1 + 1 = 2 м.

О задаче

Категория: Ряды,
Степень сложности: средняя.
Ключевые слова: 1, мяч,
Источник: Математические новеллы,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Одного старика спросили, как велика его семья. Он ответил: нас 2 брата; у меня 6 сыновей, и у каждого по 6 мальчиков; а у брата 7 сыновей, и у каждого по 7 девочек. Сколько человек в этой семье?

a) 75
b) 25
c) 100
d) 50