|
|
Задачи про середину
Продолжение списка занимательных задач про середину (страница 2)
Почему чаинки собираются в центре стакана?задача по физике
Помешав ложечкой в чашке чая, выньте ее: чаинки на дне, разбежавшиеся к краям, соберутся к середине. Почему?
Задача про точильный круг.геометрическая задача
Два человека, сложив свои сбережения, купили точильный круг. Поскольку они жили в нескольких милях друг от друга, то решили, что сначала кругом будет пользоваться старший из владельцев, а когда круг уменьшится ровно вдвое, он передаст его второму компаньону. Круг имел в диаметре ровно 22 дюйма, в середине его имелось отверстие для оси диаметром 31/7 дюйма. Чему должен равняться диаметр круга, когда его получит второй компаньон?
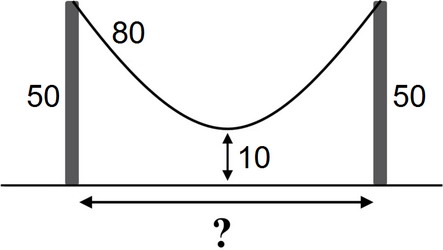
Кабель длиной 80 метров провисает между двумя столбами.геометрическая задача, задача с подвохом
Кабель длиной 80 метров провисает между двумя столбами высотой 50 метров каждый. Чему равно расстояние между столбами, если середина кабеля находится на высоте 10 метров над землей?
Средняя страница манускрипта.задача на четность
Из манускрипта (рукописи), у которого на обеих сторонах каждой страницы написан текст, удален средний лист. Две стороны этого листа пронумерованы цифрами 6 и 7. Сколько страниц содержит манускрипт?
Сколько листов осталось в книге?эффект плюс-минус один
Из книги выпал средний лист. Две стороны этого листа пронумерованы цифрами 99 и 100. Сколько листов осталось в книге?
Продолжение списка задач про середину:
1 2
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Правило ложного положения |
 Решение задачи с конца |
 Правило (принцип) крайнего |
 Инвариант |
 Чётность |
 Старинные задачи |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |