Задача на восемь королев.

Определить все способы размещения восьми королев на обыкновенной шахматной доске, состоящей из 64 клеток, таким образом, чтобы ни одна королева не могла быть взята другой, то есть расставить в 8 клетках шахматной доски столько же королев так, чтобы они не встречались попарно ни на одной линии, параллельной краям доски или одной из ее диагоналей.

Ответ

12 основных решений классической задачи о восьми ферзях показаны на рисунке.

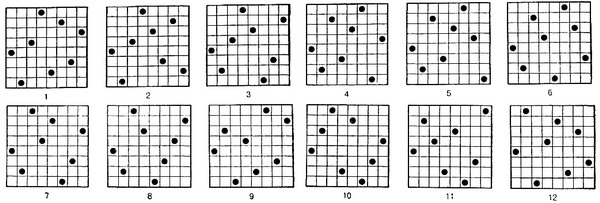
Решение задачи

Задачу о восьми ферзях впервые сформулировал в 1848 году Макс Беццель. Двенадцать основных решений (см. рисунок) опубликовал в 1850 году Франц Наук. Общее число возможных расположений, удовлетворяющих условию задачи, равно 92, причем они разбиваются на 12 групп: 11 групп из 8 расположений и 1 группу из 4 расположений. Положения внутри групп получаются из одного положения путём преобразований симметрии: отражения от вертикальной и горизонтальной осей, отражения от диагоналей доски и поворотов на 90, 180 и 270 градусов.

О задаче

Категория: Шахматные задачи, Комбинаторика,
Степень сложности: сложная.
Ключевые слова: 8, 64, клетка, ферзь, шахматы,
Источник: Математические развлечения с 55 фигурами, Задачи, ребусы, головоломки стран мира, Математическая смекалка, Математические игры и развлечения,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Сколько лет твоему сыну? - спросил один человек своего приятеля. Приятель ответил: - Если к возрасту моего сына прибавить столько же да еще половину, то будет 10 лет. Сколько же лет сыну?

a) 2 года
b) 3 года
c) 5 лет
d) 4 года